Accueil > Cours > Cours > oldies - Mecanique > Dynamique > Puissance
Puissance
Puissance des efforts extérieurs à un système en mouvement par rapport à un repère.
mardi 18 janvier 2005, par
Puissance :
Puissance des efforts extérieurs à un système en mouvement par rapport à un repère.
Soit un ensemble matériel E, en mouvement par rapport à un repère R
L’ensemble matériel E est soumis à une action mécanique représentée par un densité de force ![]() (champ de force) relative à la mesure d* en chaque point M de (E).
(champ de force) relative à la mesure d* en chaque point M de (E).
La puissance dévellopée à un instant t par l’action mécanique représenté par la densité ![]() relativement à
relativement à ![]() dans le mouvement de (E) par rapport au repère R , est
dans le mouvement de (E) par rapport au repère R , est
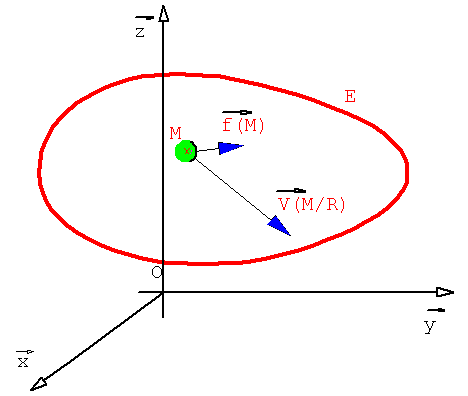
La puissance s’exprime en Watt.
![]()
Cas de la pesanteur (champ volumique)
![]()
![]()
![]()
Cas des forces de pression d’un fluide
![]()
![]()
avec ; ![]() pression au point M
pression au point M
![]() normale à la surface dS au point M
normale à la surface dS au point M
![]()
Cas particulier du solide indéformable
Soit un solide S en mouvement par rapport à un repère R
Le mouvement de S par rapport à R est caractérisé par le torseur cinématique
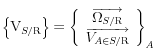
Le solide S est soumis en chaque point M à l’action mécanique caractérisée par la densité de force ![]() , cette action mécanique élémentaire est représentée par le torseur :
, cette action mécanique élémentaire est représentée par le torseur : 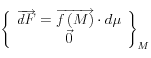
Le torseur résultant des actions sur S, réduit en A est donc :
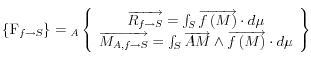
d’où la puissance dévellopée par cette action mécanique sur le solide S : ![]()
la composition des vitesses du solide nous donne :
![]()
![]()
![]()
On reconnait le comoment des torseurs cinématique et des actions mécaniques
![]()
Enoncé
La puissance mécanique développée par les actions mécaniques agissant sur un solide S au cours de son mouvement par rapport à un repère R est égale au comoment du torseur cinématique de S /R et du torseur des actions mécaniques agissant sur S.
Remarques
Le comoment des torseurs ne dépend pas du point A choisi mais les deux torseurs doivent être réduit en un même point avant d’effectuer le calcul.
On choisit le point de réduction qui permet le calcul le plus simple possible.
La valeur de la puissance calculée dépend du repère dans lequel on la calcule.
Travail
On appelle travail d’une action mécanique entre l’instant t1 et l’instant t2, la quantité obtenue en sommant la puissance développée par cette action mécanique entre ces deux instants.
![]()
l’unité du travail est le joule.
Energie potentielle
Dans certain cas le travail ne dépend pas du chemin suivi, mais uniquement des valeurs finale et initiale d’une quantité appelée énergie potentielle U.
donc ![]()
La puissance s’obtient donc par dérivation de l’énergie potentielle
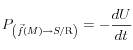
La fonction U est aussi appelée fonction de force invariable (indépendante du temps)
Puissance des efforts intérieurs à un système de solides indéformables.
Soient deux solides S1 et S2 en mouvement par rapport à un repère galiléen et liés entre eux par une liaison. La puissance totale développée par les efforts de liaison entre les deux solides (Puissance des inter-efforts) se calcule par :
![]()
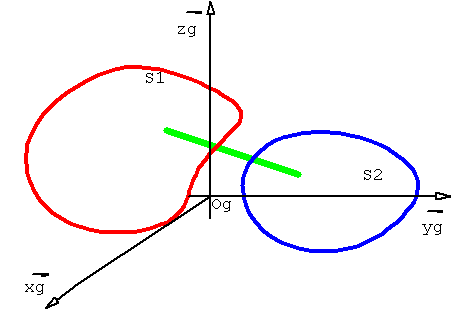
![]()
![]()
![]() (théorème des actions réciproques)
(théorème des actions réciproques)
![]()
![]()
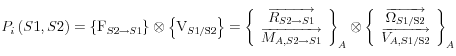
![]()
La puissance des inter-efforts de liaison est indépendante du repère choisi pour la calculer
Liaison énergétiquement parfaite
On dit qu’une liaison entre solide est énergétiquement parfaite lorsque la puissance des inter-efforts de liaison est nulle.
![]()
On se propose de déterminer à quelles conditions une liaison peut être énergétiquement parfaite
Contact ponctuel (rappel)
Soient deux solides en contact ponctuel en I
Le torseur d’action de contact s’écrit
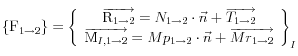
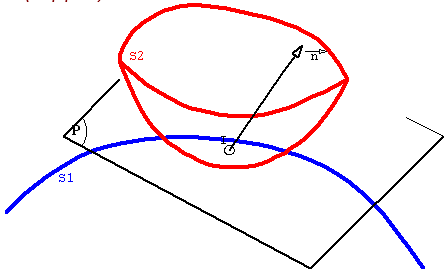
Etude de la résultante
Rappel : Lois de Coulomb
cas 1 : pas de Frottement : : f=0 ![]()
![]()
cas 2 : glissement ![]()
alors ![]() mais
mais ![]() (maintien du contact)
(maintien du contact)
donc ![]() (colinéaires) mais de sens opposés
(colinéaires) mais de sens opposés ![]()
Le module de l’effort tangentiel est s’il y a glissement ![]() avec
avec ![]() à la limite du glissement.
à la limite du glissement.
cas 3 : Roulement sans glissement, ![]()
![]() , on a
, on a ![]()
Etude du Moment : Couple de résistance au pivotement et au roulement.
Par analogie avec le frottement de glissement, on définit une résistance au pivotement et au roulement.
Les lois de contact entre deux solides sont complexes, et des lois semblables aux lois de Coulomb pour les frottements de glissement ont été formulés pour modéliser ces phénomènes
Ces couples interviennent dès que le contact ne peut plus être considéré comme ponctuel mais suivant une surface localisée.
Données
Soit deux solides S2 et S1 en contact
Le torseur cinématique du mouvement d’un solide 2 par rapport à une solide 1 s’écrit 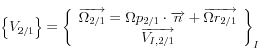 avec
avec
* ![]() normale en I au contact
normale en I au contact
* ![]() composante de pivotement du vecteur rotation de 2/1
composante de pivotement du vecteur rotation de 2/1
* ![]() composante de roulement du vecteur rotation de 2/1
composante de roulement du vecteur rotation de 2/1
Le torseur des effort transmissibles de 1->2 s’écrit :
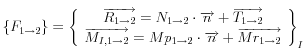 avec
avec
*![]() Composante normale
Composante normale
* ![]() Composante tangentielle
Composante tangentielle
* ![]() couple de résistance au pivotement
couple de résistance au pivotement
* ![]() couple de résistance au roulement
couple de résistance au roulement
Couple de résistance au roulement.
Les lois de Coulomb pour le roulement s’écrivent :
S2 ne roule pas sur S1 ![]()
Alors le couple de roulement vérifie la relation suivante ![]()
S2 roule sur S1 ![]()
Alors ![]() avec h Coefficient de résistance au roulement
avec h Coefficient de résistance au roulement
Couple de résistance au pivotement.
Les lois de Coulomb pour le pivotement s’écrivent :
S2 ne pivote pas sur S1 ![]()
Alors : le couple de Pivotement vérifie la relation ![]()
S2 pivote sur S1 ![]()
Alors ![]()
Pour la suite nous supposerons que ![]()
Contat ponctuel parfait ?
cas 1 : pas de Frottement : : f=0
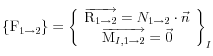 et
et 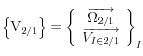 avec
avec![]()
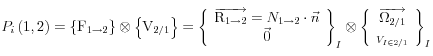
La liaison est parfaite ![]()
cas 2 : glissement ![]()
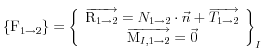
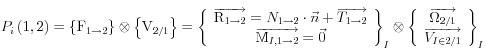
la puissance n’est pas nulle, la liaison n’est pas parfaite ![]()
cas 3 : Roulement sans glissement en I , ![]()
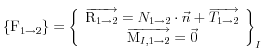 et
et 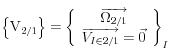
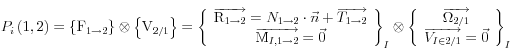
La liaison est parfaite ![]()
liaison normalisée parfaite
pour qu’une liaison normalisée soit parfaite, il faut que la puissance dissipée par la liaison soit nulle.
Théorème de l’énergie cinétique.
Cas d’un solide
énoncé
La puissance galiléenne développée par les actions mécaniques agissant sur un solide S est égale à la dérivée par rapport au temps de l’énergie cinétique galiléenne du solide .
![P_{\left( {\bar S \to S/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar S \to S/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L159xH50/fd7f6ad385311bb7942e13918b4ce82f-8e4e8.png?1440049370)
démonstration
Soit un solide S de masse m en mouvement par rapport à un repère galiléen ![]() , , le Principe Fondamental de la Dynamique appliqué à ce solide s’écrit :
, , le Principe Fondamental de la Dynamique appliqué à ce solide s’écrit :
![]() avec :
avec :
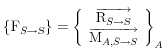 : torseur résultant des actions mécaniques extérieures à S s’exerçant sur S
: torseur résultant des actions mécaniques extérieures à S s’exerçant sur S
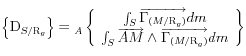 : torseur dynamique du solide S dans sont mouvement par rapport à
: torseur dynamique du solide S dans sont mouvement par rapport à ![]() ,
,
Multiplions chaque membre de l’égalité par le torseur cinématique de S par rapport au repère galiléen ![]() :
: 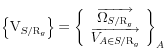
![]()
Le terme de gauche représente la puissance galiléenne développée par les actions mécaniques extérieures à S sur S.
![]()
Développons le second terme
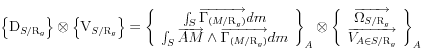
![]()
Composition des vitesses
![]()
en remplaçant dans le deuxième terme
![]()
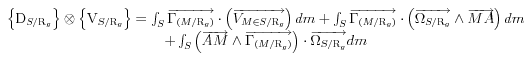
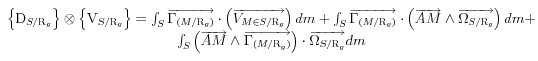
La somme des deux dernières intégrales est nulle (produits mixtes opposés )
le deuxième terme se simplifie donc : ![]()
par définition l’accélération est la dérivée par rapport au temps de la vitesse dans ![]() :
: ![\overrightarrow {\Gamma _{\left( {M/{\rm{R}}_{\rm{g}} } \right)} } = \left[ {\frac{d}{{dt}}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right]_{{\rm{R}}_{\rm{g}} } \overrightarrow {\Gamma _{\left( {M/{\rm{R}}_{\rm{g}} } \right)} } = \left[ {\frac{d}{{dt}}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right]_{{\rm{R}}_{\rm{g}} }](local/cache-vignettes/L164xH54/6cedea1c9e170de2185e36c6e1b6d11e-4995a.png?1440049371)
on remplace dans l’intégrale ![\left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \int_S {\left[ {\frac{d}{{dt}}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right]_{{\rm{R}}_{\rm{g}} } \cdot \left( {\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right)dm} \left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \int_S {\left[ {\frac{d}{{dt}}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right]_{{\rm{R}}_{\rm{g}} } \cdot \left( {\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } } \right)dm}](local/cache-vignettes/L363xH54/0ad36d6eeaded32dc3d92c9a4261f8df-6fc82.png?1440049371)
on retrouve sous le signe intégrale la forme ![]() , donc
, donc ![\left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \int_S {\frac{d}{{dt}}\left[ {\frac{1}{2}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } ^2 } \right]dm} \left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \int_S {\frac{d}{{dt}}\left[ {\frac{1}{2}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } ^2 } \right]dm}](local/cache-vignettes/L289xH50/04638d379dbc25687dd1f229b964b161-12385.png?1440052403)
on dérive un scalaire (indépendant du repère)
Compte tenu du principe de conservation de la masse on peut inverser l’intergration et la dérivation ![\left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \frac{d}{{dt}}\left[ {\int_S {\frac{1}{2}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } ^2 dm} } \right] = \frac{d}{{dt}}\left[ {T_{S/{\rm{R}}_g } } \right] \left\{ {{\rm{D}}_{S/{\rm{R}}_g } } \right\} \otimes \left\{ {{\rm{V}}_{S/{\rm{R}}_g } } \right\} = \frac{d}{{dt}}\left[ {\int_S {\frac{1}{2}\overrightarrow {V_{M \in S/{\rm{R}}_{\rm{g}} } } ^2 dm} } \right] = \frac{d}{{dt}}\left[ {T_{S/{\rm{R}}_g } } \right]](local/cache-vignettes/L368xH50/5baf5d0f264cb0d57405ec1fff9ce1a0-cad1a.png?1440063479) ,
,
on reconnait la définition de l’énergie cinétique, donc :
![P_{\left( {\bar S \to S/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar S \to S/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L159xH50/fd7f6ad385311bb7942e13918b4ce82f-8e4e8.png?1440049370)
cas de deux solides
démonstration
Soit un système matériel E composé de deux solides en mouvement par rapport à un repère galiléen.
Le théorème de la puissance appliqué a S1 donne ![P_{\left( {\bar S1 \to S1/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar S1 \to S1/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L175xH50/7b95ee3b323491b2cce37d4f6938d195-43fda.png?1440063479)
de même pour S2 ![P_{\left( {\bar S2 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar S2 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L175xH50/329b803f6ccb4c131907228701b66b83-392cf.png?1440049371)
or ![]()
et ![]()
de plus ![\frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right] + \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right] = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] \frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right] + \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right] = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L271xH50/153151c92bbf885d036e82f57add81fe-18db9.png?1440066197)
en additionnant les deux premières égalités et en remplaçant
![P_{\left( {\bar S1 \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar S2 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right] + \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar S1 \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar S2 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {S1/{\rm{R}}_{\rm{g}} } \right)} } \right] + \frac{d}{{dt}}\left[ {T_{\left( {S2/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L365xH50/007738c19ac04c240141f470dc843d75-50cae.png?1440150742)
![P_{\left( {\bar E \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S2 \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar E \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S1 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar E \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S2 \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar E \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S1 \to S2/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L436xH50/0f4d918c005020601ac57e92a94006f7-d51b1.png?1440150742)
![P_{\left( {\bar E \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar E \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S1 \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S2 \to S1/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] P_{\left( {\bar E \to S1/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {\bar E \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S1 \to S2/{\rm{R}}_{\rm{g}} } \right)} + P_{\left( {S2 \to S1/{\rm{R}}_{\rm{g}} } \right)} = \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right]](local/cache-vignettes/L436xH50/d25d4d090a385f0c81e8f98bd1ed5806-0a358.png?1440066197)
les deux premièrs termes représente la puissance galliléenne des efforts extérieurs au système E (puissance extérieure), ![]() ,
,
les deux autres la puissance des inter-efforts au système matériel E (puissance intérieure) ![]() .
.
donc la dérivée par rapport au temps de l’énergie cinétique galiléenne est égale à la somme des puissances mécaniques extérieures et intérieures au système de solides. ![\frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = P_{\left( {\bar E \to E/{\rm{R}}_{\rm{g}} } \right)} + Pi_{\left( E \right)} \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = P_{\left( {\bar E \to E/{\rm{R}}_{\rm{g}} } \right)} + Pi_{\left( E \right)}](local/cache-vignettes/L215xH50/aad7eace3652109d6cad2bdab0e32eb9-5d4ed.png?1440052403)
Cas de n solides
Enoncé
En généralisant la relation précédente :
Pour tout mouvement d’un système de solide E, la dérivée de l’énergie cinétique galiléenne de E est égale à la somme de la puissance galiléenne développée par les actions mécaniques extérieures s’exerçant sur E et de la puissance des inter-efforts entre les solides de E.
![\frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = P_{\left( {\bar E \to E/{\rm{R}}_{\rm{g}} } \right)} + Pi_{\left( E \right)} \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = P_{\left( {\bar E \to E/{\rm{R}}_{\rm{g}} } \right)} + Pi_{\left( E \right)}](local/cache-vignettes/L215xH50/aad7eace3652109d6cad2bdab0e32eb9-5d4ed.png?1440052403)
Remarques
Le théorème de l’énergie cinétique permet d’obtenir un équation différentielle du second ordre caractéristique du mouvement, cette équation n’est pas indépendante des 6 équations obtenues à partir du PFD.
L’équation obtenue est en général utilisée pour déterminer la loi d’entrée-sortie d’un mécanisme à une mobilité.
Le théorème est difficile à mettre en œuvre si les puissances intérieures ne sont pas nulle ou ne dérive pas d’une fonction de force invariable.
Intégrale première de l’énergie cinétique
Lorsque les puissances intervenant dans le théorème de l’énérgie cinétique sont nulles ou dérivent d’une fonction de force (énergie potentielle au signe près),
les puissances extérieures sont donc de la forme
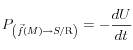 , le théorème de l’énergie cinétique s’écrit donc :
, le théorème de l’énergie cinétique s’écrit donc :
![\frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = - \frac{{dU}}{{dt}} \frac{d}{{dt}}\left[ {T_{\left( {E/{\rm{R}}_{\rm{g}} } \right)} } \right] = - \frac{{dU}}{{dt}}](local/cache-vignettes/L130xH50/b04fedb0c0d3f8beb1170f3717c8a8de-13266.png?1440049371)
en intégrant cette équation on obtient : ![]()
Remarque : cette égalité est caractéristique de la conservation de l’énergie mécanique, L’énergie mécanique se trouve sous la forme d’énergie cinétique et d’énergie potentielle par rapport à un repère galiléen.
Vos commentaires
# Le 7 janvier 2006 à 09:08, par SYL En réponse à : Puissance
Bonjour
Je voulais savoir comment peut on imprimer uniquement les cours ,seulement a partir du site(i.e sans avoir à copier coller ..) , pr les fichier qui ne sont pas en format PDF ..?
# Le 7 janvier 2006 à 11:37, par papanicola robert En réponse à : Puissance
ce n’est pas encore possible, je travaille sur la feuille de style d’impression et j’ai un souci avec les cadres
si l’un de vous peut regarder ma feuille de style, je suis preneur de toute info et modif
A+