Accueil > Cours > Cours > oldies - Mecanique > Dynamique > Cinétique masse et inertie
Cinétique masse et inertie
Effet de masse et d’inertie
dimanche 14 octobre 2012, par
La cinétique se construit à partir de la cinématique en introduisant la notion de masse.
La première partie de ce cours est donc une introduction aux effets de masse et d’inertie dans le cadre de la mécanique classique (non relativiste).
Effet de masse et d’inertie
masse
La masse caractérise la quantité de matière.
On définit la masse comme étant une grandeur complètement additive.
soient ![]() ,
,![]() deux systèmes matériels disjoints
deux systèmes matériels disjoints
alors ![]() avec
avec ![]() .
.
la masse ![]() de l’ensemble
de l’ensemble ![]() est définie par
est définie par ![]() , avec
, avec
![]() ,
, ![]() masse volumique au point P.
masse volumique au point P.
Remarque :
*si le système matériel ![]() est assimilable à une surface on parle de masse surfacique au point P :
est assimilable à une surface on parle de masse surfacique au point P : ![]() ,
, ![]() masse surfacique.
masse surfacique.
*si le système matériel ![]() est assimilable à une ligne, on parle de masse linéique au point P :
est assimilable à une ligne, on parle de masse linéique au point P : ![]() ,
, ![]() masse linéique.
masse linéique.
principe de conservation de la masse
On admet en mécanique classique que la masse est une grandeur indépendante du temps. ![]() .
.
On en déduit ![\frac{d}{{dt}}\left[ {\int_{P \in \Sigma } {\overrightarrow {f\left( {P,t} \right)} dm} } \right]_{\rm{R}} = \int_{P \in \Sigma } {\frac{d}{{dt}}} \left[ {\overrightarrow {f\left( {P,t} \right)} } \right]_{\rm{R}} dm \frac{d}{{dt}}\left[ {\int_{P \in \Sigma } {\overrightarrow {f\left( {P,t} \right)} dm} } \right]_{\rm{R}} = \int_{P \in \Sigma } {\frac{d}{{dt}}} \left[ {\overrightarrow {f\left( {P,t} \right)} } \right]_{\rm{R}} dm](local/cache-vignettes/L300xH50/93d98c39e6b26015c9bdfa11881dd956-a6121.png?1440103455) , avec
, avec ![]() un champ de vecteur défini, en tout point P de
un champ de vecteur défini, en tout point P de ![]() et à chaque date t.
et à chaque date t.
centre d’inertie
définition
On appelle centre d’inertie du système matériel ![]() , le point G défini par
, le point G défini par ![]() , avec
, avec ![]() .
.
Soit O un point quelconque :
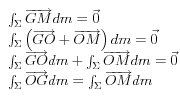
![]()
![]()
donc ![]()
on en déduit
avec ![]() cordonnées de
cordonnées de ![]() et
et ![]() coordonnées de
coordonnées de ![]() .
.
![]() ;
; ![]() ;
; ![]()
Remarque :
– si le système matériel ![]() est un solide indéformable, le centre d’inertie est un point fixe du solide.
est un solide indéformable, le centre d’inertie est un point fixe du solide.
si le système matériel possède un élément de symétrie matérielle - plan ou axe de symétrie - (du point de vue géométrique et de répartition des masses), le centre d’inertie appartient à l’élément de symétrie.
.....
Théorèmes de Guldin
Centre d’inertie d’une courbe plane
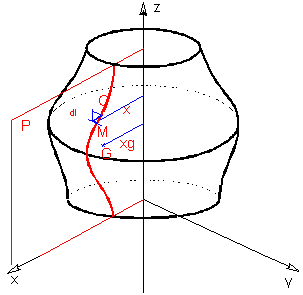
L’aire de la surface engendrée par une courbe plane tournant autour d’un axe de son plan et ne la traversant pas est égal au produit de la longueur de la courbe par le périmètre décrit par son centre d’inertie.
La courbe (C), est contenue dans le plan ![]() et ne traverse pas
et ne traverse pas ![]() .
.
On associe à la courbe (C) une masse linéique fictive :
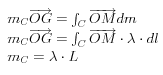
![]()
en ramenant sur l’axe x,
![]()
de plus la surface engendrée par la rotation de la courbe (C) s’écrit :
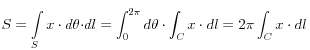
on a donc :
![]()
Centre d’inertie d’une surface plane

Le volume engendré par une surface plane tournant autour d’un axe de son plan et ne la traversant pas est égal au produit de l’aire de la surface par la longueur du périmètre du cercle décrit par son centre d’inertie.
La surface (S) est contenu dans le plan ![]() et ne traverse pas
et ne traverse pas ![]() .
.
On associe à (S) une masse surfacique .
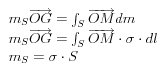
![]()
de plus le volume engendré par la surface S s’écrit :
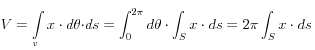
d’où :
![]()
Remarque :
L’utilisation des théorèmes de Guldin permet de simplifier le calcul de position du centre d’inertie dans la mesure où l’on connaît les caractéristiques du volume ou de la surface balayée.
Travaux dirigés
CF TD
Remarque :
Le centre d’inertie est confondu avec centre de gravité dans le cas d’un champ de pesanteur uniforme.
Vos commentaires
# Le 15 décembre 2006 à 11:15 En réponse à : Cinétique masse et inertie
un système matriel assimilable a une ligne. dm=lambda*ds.je pense que c dl a la place de ds