Accueil > Cours > Cours > oldies - Mecanique > Statique > Modélisation des actions mécaniques
Modélisation des actions mécaniques
mercredi 19 janvier 2005, par
Actions mécaniques
définition
On appelle action mécanique tout phénomène susceptible de :
- provoquer ou modifier le mouvement d’un solide, ou d’un ensemble de solides ;
- maintenir un corps au repos
- produire des déformations d’un solide.
classification
On distingue 2 types d’action mécanique :
– les actions mécaniques de contact (liaisons de contact entre solides, pression,...) ;
– les actions mécaniques à distance (champ de pesanteur, force électromagnétique,...).
Le premier type d’action est une action qui s’applique sur la surface du solide (action surfacique), le second s’exerce au niveau de son volume (action volumique).
On distingue aussi les actions extérieures et intérieures à un système de solides.
Modélisation
L’analyse des actions mécaniques ne peut se faire qu’en utilisant des modèles pour représenter les actions et leurs effets sur le solide. on distingue principalement deux modèles pour représenter et étudier les actions mécaniques, le modèle local et le modèle global.
Le modèle local permet d’étudier l’action et son effet en tout point de la zone où elle s’exerce : étude des pressions de contact, contraintes dans les matériaux, déformation du solide,
Dans le modèle global on associe à l’action mécanique un torseur (dit Torseur d’Action Mécanique). Ce modèle fait disparaître l’effet local de l’action mais rend son utilisation pratique pour l’étude de l’équilibre ou de la dynamique.
Ces deux modèles ne sont pas interchangeables, si on peut déterminer le torseur d’action mécanique à partir de la répartition locale des efforts, on ne peut faire le travail inverse sans faire des hypothèses sur la répartition.
– Modèle local :
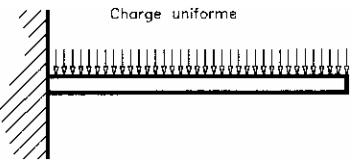
– Modèle global
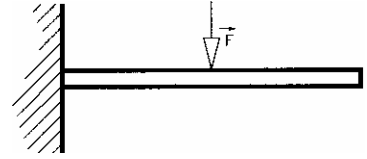
La charge uniforme est remplacée par l’effort équivalent
Actions volumiques ou à distance
On appelle action à distance toute action qui s’applique sur les solides ou les fluides sans contact (action de la pesanteur, actions électromagnétiques,...).
Modélisation locale
l’ensemble des vecteurs ![]() est appelé le champ de force de l’action.
est appelé le champ de force de l’action.
En un point particulier A le torseur d’action mécanique s’écrit :

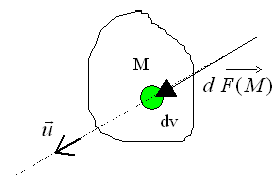
Pour chaque point M on définit un volume élémentaire (dV). L’action élémentaire s’exerçant sur le volume dV a pour expression :
![]()
![]() : fonction de répartition volumique d’effort ;
: fonction de répartition volumique d’effort ;
![]() : Vecteur unitaire de la direction de l’action.
: Vecteur unitaire de la direction de l’action.
Modélisation globale - torseur associé ;
Torseur d’action mécanique
En un point particulier A le torseur d’action mécanique s’écrit :
 ou (D) est le domaine sur lequel s’applique l’action (surface ou volume)
ou (D) est le domaine sur lequel s’applique l’action (surface ou volume)
Modèle global
L’action élémentaire s’exerçant sur le volume dV a pour expression :
![]()
d’ou le torseur d’action mécanique pour au point A

Le torseur d’action globale sur le volume V s’écrit :

cas de la pesanteur
![]() avec
avec ![]() la masse volumique du matériau et g l’accélération de la pesanteur au point M.
la masse volumique du matériau et g l’accélération de la pesanteur au point M.
![]() : vecteur unitaire descendant.
: vecteur unitaire descendant.
le champ de force de pesanteur est un champ de force parallèles
on a donc :
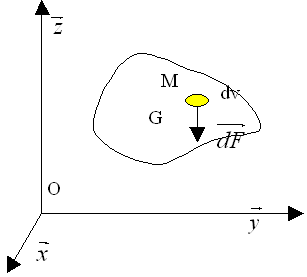

si![]() (matériau homogène)
(matériau homogène)

et ![]() (masse du solide)
(masse du solide)
– Centre de gravité
IL existe un point G, tel que le torseur de pesanteur est réductible à un glisseur.
Le centre de gravité (ou centre d’inertie) est tel que le moment en G du torseur d’action de pesanteur est nul.
Le centre de gravité est sur l’axe central du torseur.
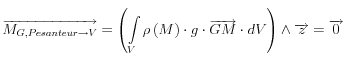
ce moment est nul si : 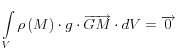
soit O un point de l’espace, on peut écrire
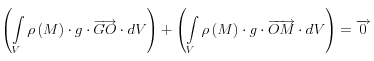
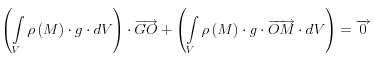
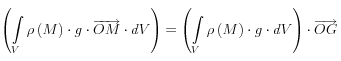
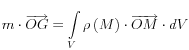
et finalement : ![]()
Actions de contact (actions surfaciques)
On appelle action surfacique ou action de contact, toute action mécanique qu’exercent deux solides l’un sur l’autre ou un solide et un fluide au niveau de leur surface de contact commune

Modélisation locale
Pour chaque point M au contact on définit une surface élémentaire (dS). L’action élémentaire s’exerçant sur l’élément de surface dS a pour expression :
![]()
![]() : fonction de répartition surfacique de l’effort ;
: fonction de répartition surfacique de l’effort ;
![]() : Vecteur unitaire de la direction de l’action.
: Vecteur unitaire de la direction de l’action.
On décompose l’effort en général en un effort normal à la surface de contact et un effort contenu dans le plan tangent à la surface.
![]()
![]() : pression de contact au point M
: pression de contact au point M
![]() : vecteur unitaire normal au plan tangent dirigé vers l’extérieur du solide étudié.
: vecteur unitaire normal au plan tangent dirigé vers l’extérieur du solide étudié.
![]() :répartition tangentielle de l’effort.
:répartition tangentielle de l’effort.
![]() : vecteur unitaire contenu dans le plan tangent.
: vecteur unitaire contenu dans le plan tangent.
Modélisation globale - torseur associé ;
Le torseur au point associé à une action de contact (répartition surfacique) du solide 2 sur le solide 1 est donc :


Pour aller plus loin, il est nécessaire de préciser la nature du contact entre les deux solides (avec ou sans frottements).
Vos commentaires
# Le 7 mai 2005 à 12:19, par Nico En réponse à : > Modélisation des actions mécaniques
Merci pour ce cours, ça aide pour les révisions de trouver un endroit où les cours sont plus propres que les miens :-)
Cependant les torseurs concernant la pesanteur me semblent erronés :
– d’abord, les torseurs définissent la pesanteur selon le vecteur z, ce qui est conforme aux conventions, tandis que le dessin, de manière assez inhabituelle, représente y comme la verticale.
– Encore moins conforme aux conventions est le signe de ce vecteur : g, dV et rhô(M) sont habituellement des valeurs absolues. Le vecteur unitaire devrait donc être -z, ou -y selon ce dessin.
– Enfin, un des moments présente un produit vectoriel suivit d’une multiplication par un vecteur, ce qui ne peut représenter un moment, car le moment est un vecteur et non un scalaire.
Enfin, merci encore.
P.S : je soupçonne mon propre prof d’utiliser ce site pour faire son cours. Mais il a raison.
# Le 7 mai 2005 à 13:25, par papanicola robert En réponse à : > Modélisation des actions mécaniques
merci de cette lecture attentive, j’ai corrigé la figure et les quelques torseurs "douteux"
PS : je me suis aussi beaucoup inspiré du reste du monde
A+
# Le 14 mai 2005 à 21:27, par Nico En réponse à : > Modélisation des actions mécaniques
Euh, une erreur demeure : dans le torseur
Fpesanteur->V, on trouve encore
AM vectoriel z * z pour le moment, AM et z étant des vecteurs, ce qui ferait hurler mon prof de maths...
Enfin, merci encore, j’ai donné l’adresse aux copains, ça a servi pour réviser le contrôle.
# Le 21 mai 2005 à 16:41, par papanicola robert En réponse à : > Modélisation des actions mécaniques
Corrigé
c’était juste pour faire rire ton prof de math
A+
# Le 1er janvier 2006 à 20:49 En réponse à : 1 requête
pourait on avoir les cours de statique au forma pdf ?
# Le 1er janvier 2006 à 21:00, par papanicola robert En réponse à : 1 requête
non
un petit copier/coller dans word ou open office permet d’avoir une trace info
A+
# Le 27 octobre 2006 à 11:57, par Abdelkader znasni En réponse à : Modélisation des actions mécaniques
pourait on avoir le cours sur la statique, modélisation des actions mécaniques avec des exo. corrigés format word ou pdf ?
# Le 11 octobre 2007 à 19:26, par Bulgroz En réponse à : Modélisation des actions mécaniques
Très intéressant, mais pourriez-vous SVP définir la différence entre actions mécaniques, forces et efforts
Si j’ai bien compris actions mécaniques c’est pour forces, moment, couples, etc... (force étant plutôt pour des interactions élémentaires,
mais pour "effort", je n’arrive pas à trouver une définition nette et précise.
Merci d’avance.
# Le 11 octobre 2007 à 22:36, par papanicola robert En réponse à : Modélisation des actions mécaniques
en fait j’évite d’utiliser avec mes étudiants le terme « force » qui justement est très difficile à définir, je préfère celui d’action mécanique et dans le cas d’une modélisation par Torseur, je dirai Torseur d’Action Mécanique.
le terme générique « force » (que je n’utilise pas ) correspond en général à la résultante de cette action mécanique (en Newton).
j’espère avoir répondu
# Le 12 octobre 2007 à 14:38, par Bulgroz En réponse à : Modélisation des actions mécaniques
Hélas pas complètement, car c’est vraiment le mot "effort" qui me pose personellement problème :
Qu’est-ce qu’un effort ? Quelle est la diférence avec une action mécanique ?
Je l’ai vu assez souvent intervenir dans l’expression "efforts transmissibles" et je m’étais dit qu’il devait s’agir des actions mécaniques imposées par l’extérieur pour actionner le mécanisme, mais comme j’ai vu que certains parlaient aussi d’"efforts intérieurs", cela m’a mis dans l’expectative !
En tout cas merci pour la rapidité de la réponse précédente !
PS : pour ma part, étant plus physicien que mécanicien de formation, j’avais l’habitude de définir d’abord les interactions puis les forces, puis les actions mécaniques, mais, voulant me rapprocher du point de vue des mécaniciens, j’ai très récemment changé cela pour donner ce qui suit, dans lequel effectivement, une certaine confusion peut s’installer entre forces et actions mécaniques. C’est pour cela que je me suis remis à la recherche de définitions !
Définition : deux systèmes (S1) et (S2) sont dits en interaction, si l’on peut trouver dans l’un, une modification (de position, d’orientation de structure ou de propriété interne) qui entraîne une modification dans l’autre (modification du mouvement de l’autre ou déformation de l’autre). (ex : aimant et boussole). On dira alors que celui qui entraîne une modification de l’autre exerce une action mécanique sur l’autre. On dit donc que (S1) exerce une action mécanique sur (S2) si (relativement à un référentiel), les mouvements de (S2) (ou les déformations de (S2), ou les mouvements de n’importe quelle partie de (S2), ou le fait pour (S2) d’être au repos) sont différent(e)s selon que (S1) est présent ou absent.
Définition 2 : on appelle force la grandeur mathématique décrivant une interaction capable de produire ou de modifier le mouvement d’un point matériel. La différence avec ce qui précède est que l’usage de la notion de force brise la symétrie qui existait entre le statut des deux systèmes en interaction : on parle de la force exercée par un système sur un autre et non plus simplement de l’interaction entre deux systèmes. La force est décrite par un pointeur, c’est-à-dire l’association d’un vecteur et d’un point d’application.
Remarque : Toutes les interactions connues (à part peut-être les forces à l’origine du confinement des quarks dans les hadrons…) ont la propriété de décroître avec la distance, ce qui permet de concevoir un système isolé comme une limite pour les grandes distances de séparation.
Postulat 1 : l’ensemble des forces élémentaires exercées par les éléments constitutifs d’un système continu (S1) sur un système continu (S2) est représentable par un torseur F_(S1)->(S2) appelé torseur des actions mécaniques de (S1) sur (S2), composé par la résultante des forces exercées par (S1) sur (S2) et d’un champ de moment de ces forces.
Dans ce cadre, les forces sont représentées par des glisseurs et ne sont donc plus que des cas particuliers d’actions mécaniques, tout comme les couples (de forces) d’ailleurs !
Puis j’embraye sur la modélisation des actions mécaniques sur un milieu continu avec la notion de densité massique de forces etc...
# Le 12 octobre 2007 à 17:45, par Bulgroz En réponse à : Modélisation des actions mécaniques
Désolé pour les sauts de paragraphes qui ont disparus dans le message ci-dessus, ce qui n’en facilite pas la lecture !
Est-ce que "effort" ne serait pas synonyme de "contrainte", c’est-à-dire de "force par unité de suface" ou de "densité surfacique d’action mécanique" ?
# Le 12 octobre 2007 à 17:46, par Bulgroz En réponse à : Modélisation des actions mécaniques
Désolé pour les sauts de paragraphes qui ont disparus dans le message ci-dessus, ce qui n’en facilite pas la lecture !
Est-ce que "effort" ne serait pas synonyme de "contrainte", c’est-à-dire de "force par unité de suface" ou de "densité surfacique d’action mécanique" ?
# Le 12 octobre 2007 à 22:16, par papanicola robert En réponse à : Modélisation des actions mécaniques
ReSalut
de rien, je reçois en mail à chaque post dans les forums, mais je ne réponds pas toujours !
je suis d’accord avec ta présentation de la "force", c’est globalement la mme que moi.
# Le 12 octobre 2007 à 22:35, par papanicola robert En réponse à : Modélisation des actions mécaniques
il faut deux retrour chariot comme sous latex, tu as d’ailleurs la possibilité d’écrire des formules mathématiques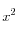
<math> $ x^2 $ </math>donneEst-ce que "effort" ne serait pas synonyme de "contrainte", c’est-à-dire de "force par unité de suface" ou de "densité surfacique d’action mécanique" ?
Non, pas pour moi, si je dois lui associer une unité, se serait des Newtons
Je dis aussi efforts transmissibles, lorsque je veux parler des actions transmissibles par une liaison,mais c’est une facilité de langage
Je crois que dans la majorité des cas, ce vocabulaire est utilisé dans un sens usuel pour éviter des répétitions avec le sens d’action mécanique.
A+
Ps- j’ai lancé un petit sondage sur la liste des profs de prépas, et si une synthèse se dégage, je préciserai ici les définitions
# Le 21 octobre 2007 à 15:37, par Bulgroz En réponse à : Modélisation des actions mécaniques
Merci pour le sondage.
J’attends avec grand intérêt le résultat !!!
# Le 23 octobre 2007 à 19:19, par Bulgroz En réponse à : Modélisation des actions mécaniques
C’est encore moi ! ;-)
Je viens de retrouver dans d’anciennes notes de cours d’élasticité pour géologues une remarque selon laquelle les efforts seraient des actions mécaniques internes au système tandis que les sollicitations seraient des actions mécaniques causées par l’exterieur du système.
Cela devait probablement provenir du livre de Lliboutry sur le sujet mais je ne l’ai plus sous la main pour contrôler.
Un avis là dessus ?
# Le 11 septembre 2011 à 17:13, par PeterSmith En réponse à : Modélisation des actions mécaniques
I 100 percent agree with you. I tried to do this. And it was amazing. For example I need to write my essay for me in college, but I use term paper writing service and have all day free only for myself.
# Le 1er novembre 2011 à 10:18, par Nathpic En réponse à : Modélisation des actions mécaniques
Merci pour cet article vraiment très intéressant, surtout pour moi qui ai du mal avec la modélisation.
# Le 20 avril 2012 à 14:16, par JamiDelorme En réponse à : Modélisation des actions mécaniques
Je suis d’accord avec vous ! C’est ressembler à la research papers par écrit. Dans mon collège, c’est très intéressant discipline importante. blog de Nice