Accueil > Cours > TD > Automatique > Asservissement > Diagrammes de Bode et Black

Diagrammes de Bode et Black

dimanche 2 janvier 2005, par papanicola robert

– TD1 : à partir des equations différentielles
Soit un système d’entrée e(t) , de sortie y(t) décrit par le système d’équations suivantes :
\frac{{{\rm{d}}^{\rm{2}} {\rm{y(t)}}}}{{{\rm{dt}}^{\rm{2}} }} + 110 \cdot \frac{{{\rm{dy(t)}}}}{{{\rm{dt}}}} + 1000 \cdot {\rm{y(t)}} = \frac{{{\rm{dx(t)}}}}{{{\rm{dt}}^{} }} + {\rm{30}} \cdot {\rm{x(t)}}
\frac{{{\rm{dx(t)}}}}{{{\rm{dt}}}} + {\rm{x(t) = k}} \cdot {\rm{e(t)}}

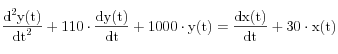
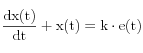
x(t) est une variable interne au système.
On suppose x(0)=y(0)=e(0)
Donner la fonction de transfert du système.

Tracer les diagrammes de Bode
Tracer le diagramme de black]

– TD2 : à partir d’un relevé fréquentiel
On donne le tableau de valeur suivant pour la fonction h(p)

pulsation hdb phase
0.10 38 -92
0.26 30 -95
0.67 21 -104
1.37 14 -117
2.81 6 -138
3.56 3 -147
4.52 -1 -155
5.74 -4 -163
9.24 -12 -179
23.95 -30 -211
48.94 -46 -235

Tracer son diagramme de Black.
Tracer les diagrammes de Bode