Accueil > Cours > TD > Mécanique > Dynamique > Etude cinétique simplifiée d’une moto

Etude cinétique simplifiée d’une moto

lundi 10 octobre 2005, par papanicola robert

Données

Le système étudié est un modèle rudimentaire de moto. Il se compose de trois sous parties :
–  La roue arrière (S1) de centre C1 ;
–  la roue avant (S2) de centre C2 ;
–  l’ensemble chassis_motocycliste (S3), considéré comme un système indéformable de centre d’inertie C3.

– Le centre d’inertie de S=S1\cup S2\cup S3 est noté C ;
– La masse totale de S est M_{s}  ;
– La masse d’une roue est m_{r} , le rayon R ;
– Les roues sont en contact avec le sol en I1 et I2

M_{s} =150kg , m_{r} =5kg ,
a=0,45m , b=0,55m , c=0,75m , R=0,30m

– Le repère R0 \left(O,\vec{x}_{0} \vec{y}_{0} ,\vec{z}_{0} \right) , est un repère galiléen lié au sol.
– le repère R1 \left(C_{2} ,\vec{x}_{1} ,\vec{y}_{1} ,\vec{z}_{0} \right) est lié à la roue(S1) : \displaystyle \left(\vec{x}_{0} ,\vec{x}_{1} \right)=\alpha

– le repère R2 \left(C_{2} ,\vec{x}_{2} ,\vec{y}_{2} ,\vec{z}_{0} \right) est lié à la roue(S2) : \displaystyle \left(\vec{x}_{0} ,\vec{x}_{2} \right)=\beta

Hypothèses

Le problème est supposé plan, c’est à dire que le centre d’inertie reste dans le plan vertical passant par les points de contact des roues avec le sol.

Questions

– Répartition des masses dans un roue

Soit m_{r} la masse d’une roue ; on suppose que la moitié de cette masse est répartie sur un disque homogème d’épaisseur négligeable et de rayon R, et l’autre moitié sur un cercle homogème de rayon R entourant le précédent.

  1. Quelle est la forme de la matrice d’inertie au centre d’inertie ?, précisez la base ?
  2. Déterminez les différents coefficients de la matrice
    (On pourra si nécessaire, utiliser , masse surfacique pour le disque et , masse linéïque pour le cercle.)
  3. A.N

– Cinétique

On suppose maintenant que les deux roues roulent sans glisser sur un plan horizontal. On donne la vitesse de C par rapport au sol : \overrightarrow{V_{C\in S/{\rm R0}} }=v\cdot \vec{x}_{0}

  1. Explicitez la condition de non glissement pour chacune des roues,
  1. Déduisez-en 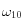\omega _{10} la vitesse de rotation de la roue 1 et 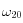\omega _{20} la vitesse de rotation de la roue 2 en fonction de R et de v.
  2. Donnez les torseurs cinématiques des solides (S1) , (S2), (S3) par rapport au repère lié au sol
  3. Déterminez les torseurs cinétiques de ces mêmes solides dans leur mouvement par rapport au repère R0
  4. Déterminez la position du centre d’inertie C3 de (S3) puisque C3 est le centre d’inertie de (S3) on peut écrire par définition du centre d’inertie : \sum \limits _{i=1}^{3}m_{i} \overrightarrow{CC_{i} } =\vec{0}
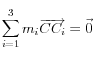
  5. Déterminez le torseur cinétique de l’ensemble (S).
  6. Déterminez l’énergie cinétique 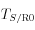T_{S/{\rm R0}} de l’ensemble (S) dans son mouvement par rappport à R0
  7. A.N v=100km/h

Vos commentaires