Accueil > Cours > TD > Colles informatiques > Maple > Procédures Maple d’étude des systèmes linéaires

Procédures Maple d’étude des systèmes linéaires

mercredi 7 juin 2006, par papanicola robert, Roger Lhermet

– Papanicola Robert : version initiale
– Lhermet Roger :Modifications et évolutions

Version 13 avril 2005
Cette nouvelle version intègre la mise en couleur des diagrammes de Bode.

Bibliothèque de procédures Maple chargée avec la commande with(automatique).

Nécessite les bibliothèques plots et inttrans chargées par les commandes with(plots) et with(inttrans).

– bodeamp(FT, \omega_{\min } , \omega_{\max }, nbpoints)

  • Trace le diagramme de Bode du gain.
  • FT : fonction de transfert,
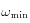  • \omega_{\min } : pulsation minimale,
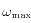  • \omega_{\max } : pulsation maximale,
  • nbpoints : nombre de points du tracé

– bodeasymp(FT, \omega_{\min } , \omega_{\max }, nbpoints) ou bodeasymp(FT, \omega_{\min } , \omega_{\max }, nbpoints, couleur)

  • Trace le diagramme de Bode du gain asymptotique.

Pour avoir les deux graphes du gain, réel et asymptotique, utiliser la commande maple display(graphe1,graphe2)

– bodePhy(FT, \omega_{\min } , \omega_{\max }, nbpoints)

  • Trace le diagramme de Bode de la phase.

– bodeasymPhy(FT, \omega_{\min } , \omega_{\max }, nbpoints) ou bodeasymPhy(FT, \omega_{\min } , \omega_{\max }, nbpoints, couleur)

  • Trace le diagramme de Bode de la phase asymptotique.

Pour avoir les deux graphes de la phase réelle et asymptotique, utiliser la commande maple display(graphe1,graphe2)

– bode(FT, \omega_{\min } , \omega_{\max }, nbpoints)

  • Trace le diagramme de Bode du gain et le diagramme de Bode de la phase.
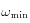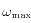  1. black(FT, \omega_{\min } , \omega_{\max }, nbpoints)
  • Trace le diagramme de Black.
  1. blackpoint(FT,listedepoints)
  • listedepoints : liste de valeurs de pulsation.
  • Trace le diagramme de Black sous forme de points à partir d’une liste de pulsation, indique sur la courbe la pulsation du point.
  • A superposer avec la procédure précedente à l’aide la commande maple display .

– blacketfond(FT, \omega_{\min } , \omega_{\max }, nbpoints,[\Phi_{\min } .. \Phi_{\max } , A_{\min } .. A_{\max }])

  • Trace le diagramme de Black avec le fond Nickols.
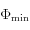  • \Phi_{\min } : déphasage minimale
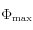  • \Phi_{\max } : déphasage maximale,
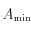  • A_{\min } : gain en dB minimal,
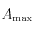  • A_{\max } : gain en dB maximal,

– nyquist(FT, \omega_{\min } , \omega_{\max }, nbpoints)

  • Trace le diagramme de Nyquist, échelles différentes sur les deux axes.

– nyquist1(FT, \omega_{\min } , \omega_{\max }, nbpoints ,[Re_{\min } .. Re_{\max } , Im_{\min } .. Im_{\max } ])

  • Trace le diagramme de Nyquist avec une fenêtre définie,même échelle sur les deux axes.
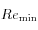  • Re_{\min } : Réel minimal,
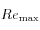  • Re_{\max } : Réel maximal,
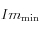  • Im_{\min } : Imaginaire minimal,
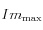  • Im_{\max } : Imaginaire maximal,

– ftbf(FTCD,FTCR)

  • Retourne la FTBF à partir de la chaîne directe et de la chaîne de retour, pour un retour unitaire faire FTCR = 1.

– ftbo(FTBF)

  • Retourne la FTBO à partir de la FTBF pour un retour unitaire.

– reptemp(entrée,FT,t{\max })

  • Trace la réponse temporelle à partir de la fonction temporelle de l’entrée, l’entrée et la sortie sont superposées sur le graphe.

– routh(poly)

  • Rempli le tableau de Routh à partir du polynôme poly.
  1. Gain(FT)(\omega)
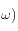
  • Retourne le gain en dB de la fonction de transfert FT pour la valeur de la pulsation égale à \omega.

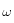– Phy(FT)(\omega)

  • Retourne le déphasage en degrés de la fonction de transfert FT pour la valeur de la pulsation égale à \omega.

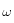Vos commentaires