Accueil > Cours > TD > Mécanique > Cinématique > Approche de la cinématique de la marche
Approche de la cinématique de la marche
samedi 10 décembre 2005, par
Exercice 1 : Analyse d’un mouvement de flexion-extension du genou
Rq : Les justifications attendues dans cet exercice sont relativement succinctes et font le plus souvent intervenir peu de calcul.
Répondre à cet exercice sur ce document - Si une donnée vous semble erronée ou manquante, poursuivez avec vos propres hypothèses en les justifiant.
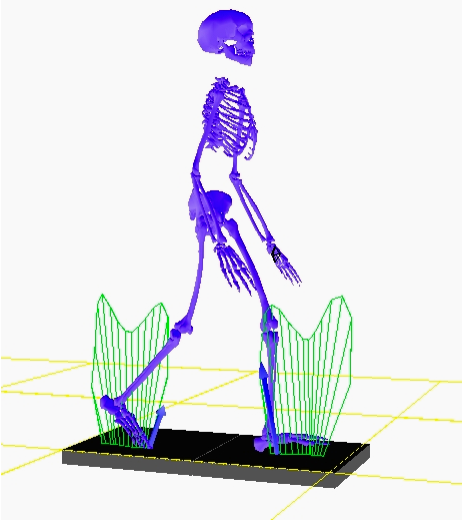
Pour analyser la cinématique articulaire d’un patient, on réalise l’examen suivant :
On demande au patient de se placer en appui bipodal (sur ses deux pieds) puis de réaliser une flexion puis une extension des genoux sans bouger les pieds. Lors de ce mouvement, on admet que le plan sagittal (le plan de symétrie du corps humain) reste plan de symétrie du mouvement et que les axes des membres inférieurs se déplacent dans un plan parallèle au plan sagittal de symétrie.
Pour analyser le mouvement, on équipe le patient de marqueurs (ce sont des repères identifiés par des caméras en temps réel, figure n°1) et on enregistre la position des marqueurs au cours du temps à l’aide d’un système optoélectronique. Les coordonnées des marqueurs sont fournies dans le repère Ro représenté sur la figure n°2.
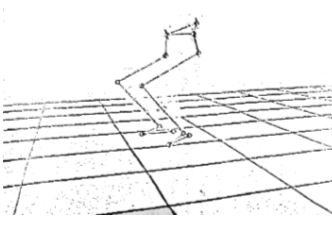
flexion-extension
|

analyse de la marche
|
Chaque segment osseux est assimilé à un solide indéformable (figure n°2) et les articulations sont représentées par des liaisons pivot d’axe ![]()
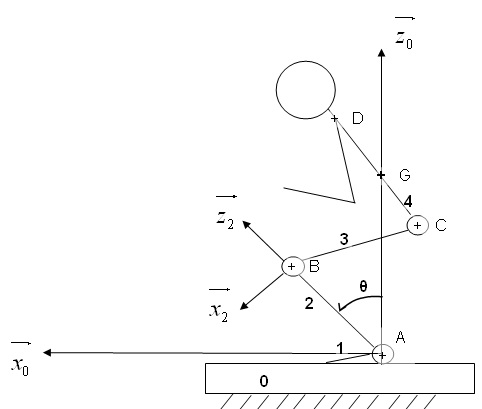
figure 2 : modele cinématique
|
Pour le tibia :
AB=35cm=L2 Pour le fémur : BC=40cm=L3 |
I/ Mouvements :
1/ Quel est le mouvement de 1/0 ? de 2/1 ? de 3/2 ? de 4/3 ?
II/ Etude de la cinématique du centre de gravité du sujet G
Le système optoélectronique fournit les coordonnées du centre de gravité G au cours du temps dans Ro. Ces coordonnées s’expriment sous la forme de fonction algébrique du temps.
– ![]()
– ![]()
– ![]() pour t compris entre 0 et 1s
pour t compris entre 0 et 1s
– ![]() pour t compris entre 1 et 2 s
pour t compris entre 1 et 2 s
– ![]() pour t compris entre 2 et 3 s
pour t compris entre 2 et 3 s
2/ Décrire la trajectoire de G dans Ro. Justifier que la trajectoire ne pourrait être différente (si le patient se déplace « assez lentement »)et tracer le graphe ZG(t) pour t compris entre 0 et 3s.

graphe
|
3/ Donner ![]() en fonction du temps. Représenter la valeur algébrique de cette vitesse sur le graphe suivant. Identifiez sur le graphe la période d’extension et la période de flexion du genou.
en fonction du temps. Représenter la valeur algébrique de cette vitesse sur le graphe suivant. Identifiez sur le graphe la période d’extension et la période de flexion du genou.

graphe
|
4/ Donner ![]() en fonction du temps
en fonction du temps
III/ Etude de la cinématique du tibia 2
Le système optoélectronique fournit les coordonnées de B (en m) dans Ro au cours du mouvement avec une acquisition toutes les 0.25s.
| t | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 |
| XB | 0 | 0.0175 | 0.0695 | 0.1282 | 0.1678 | 0.1903 | 0.2 |
| YB | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
et
| t | 1.75 | 2 | 2.25 | 2.5 | 2.75 | 3 |
| XB | 0.1903 | 0.1678 | 0.1282 | 0.0695 | 0.0175 | 0 |
| YB | 0 | 0 | 0 | 0 | 0 | 0 |
5/ Tracer et définir sur la figure 2 (page 1) la trajectoire de B dans Ro.
6/ Donner l’expression du vecteur position ![]() dans le repère R2 défini sur la figure n°2.
dans le repère R2 défini sur la figure n°2.
7/ Donner l’expression du vecteur position ![]() dans le repère Ro en fonction de l2 longueur du tibia et θ angle défini sur la figure 2.
dans le repère Ro en fonction de l2 longueur du tibia et θ angle défini sur la figure 2.
On calcule l’angle θ(t) et on obtient les expressions algébriques suivantes :
– ![]() pour t compris entre 0 et 0.5s
pour t compris entre 0 et 0.5s
– ![]() pour t compris entre 0.5 et 2.5s
pour t compris entre 0.5 et 2.5s
– ![]() pour t compris entre 2.5 et 3s
pour t compris entre 2.5 et 3s
9/ Calculer le vecteur vitesse de rotation ![]() et tracer son évolution en fonction de t.
et tracer son évolution en fonction de t.

graphe
|
10/ Calculer ![]() exprimée dans le repère R2. Exprimer ensuite le résultat dans R0. Donner la valeur algébrique de la vitesse pour t=1s.
exprimée dans le repère R2. Exprimer ensuite le résultat dans R0. Donner la valeur algébrique de la vitesse pour t=1s.
IV/ Etude de la cinématique du fémur 3 (toutes les constructions graphiques de cette partie se feront figure 4)
La figure n°4 représente la position du sujet au temps t=1s.
11/ Sur le schéma de la figure n°4 (ci-dessous), tracer ![]() et
et ![]() à t=1s.
à t=1s.
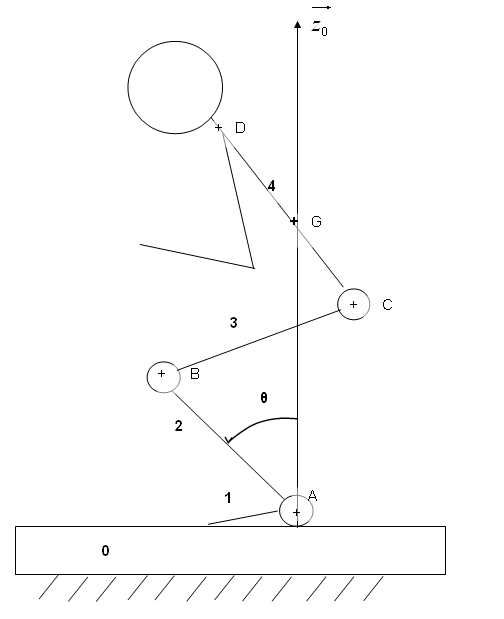
figure 4
– Echelle des distances : 1mm↔1cm
– Echelle des vitesses : 0.5 cm ↔0.1m/s |
12/ En utilisant l’équiprojectivité sur le solide 4, déterminer une droite sur laquelle doit se trouver l’extrémité du vecteur ![]() .
.
13/ Quelle est la relation entre ![]() et
et ![]() ? En utilisant l’équiprojectivité sur le solide 3, déterminer une droite sur laquelle doit se trouver l’extrémité du vecteur
? En utilisant l’équiprojectivité sur le solide 3, déterminer une droite sur laquelle doit se trouver l’extrémité du vecteur ![]() .
.
14/ Quelle relation existe-t-il entre ![]() et
et ![]() ? Déduisez-en le tracé de
? Déduisez-en le tracé de ![]() . Donner ¨
. Donner ¨![]() .
.
15/ Tracer le CIR I3/0 du mouvement de 3/0 sur la figure 4. Justifier
16/ En déduire Ω(3/0)
17/ Calculer alors Ω(3/2)
IV/ Etude de la cinématique du tronc 4
Précédemment, vous avez déterminé graphiquement ![]() et
et ![]() à t=1s. Reporter ces vitesses sur la figure 5 ci-dessous.
à t=1s. Reporter ces vitesses sur la figure 5 ci-dessous.
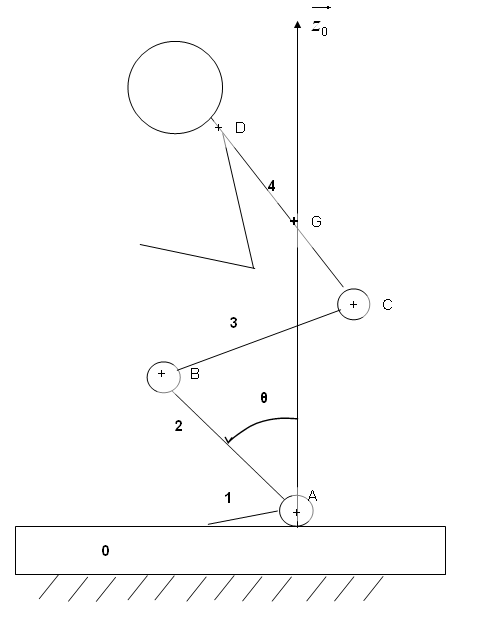
figure 5
– Echelle des distances : 1mm↔1cm
– Echelle des vitesses : 0.5 cm ↔0.1m/s |
18/ Déterminer graphiquement ![]() (la vitesse vectorielle des cervicales) à t=0.5s.
(la vitesse vectorielle des cervicales) à t=0.5s.
19/ Déterminer ![]() .
.
V/ Question subsidiaire...
20/ Connaissant ![]() et le théorème des 3 plans glissants, déterminer le CIR de 3/0.
et le théorème des 3 plans glissants, déterminer le CIR de 3/0.