Sphéricône

On obtient un sphéricône à partir d’un double-cône de 90° d’angle au sommet coupé en deux par un plan passant par l’axe puis recollé après une rotation de 90°.
On se propose de déterminer les caractéristiques cinétiques du sphéricône et de les comparer à celle du double-cône.

– Déterminer par des considérations géométriques la position du centre d’inertie G et la forme de la matrice d’inertie du sphéricône en G (préciser la base).
Le sphéricône peut se décomposer en 4 demi-cônes de rayon R et de demi-angle au sommet 45°

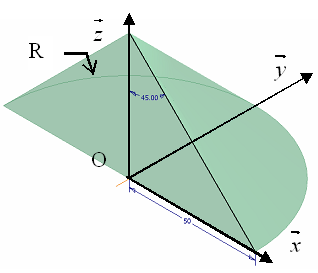
– précisez la forme de la matrice d’inertie d’un demi-cône en O dans la base (x, y, z).

– Déterminez la matrice d’inertie de demi - cône en ne calculant que les termes utiles pour la matrice du sphéricône.

– Déterminer celle du sphéricône.